ИННОВАЦИИ БИЗНЕСУ

Наименование инновационного проекта

«Производство нового технического устройства «Фотоаппарат газоразрядный»

Рекомендуемая область пременения

Медицина, биология, ветеринария, растениеводство, сельское хозяйст-во, пищевая промышленность, дефектоскопия, криминалистика, экология.

Назначение, цели и задачи проекта

Основное назначение проекта – разработка и создание новых и альтернативных методов и средств диагностики и контроля посредством нового переносчика информации – газоразрядной плазмы.

Создание высокоэффективных и информационно-емких регистрирующих сред для фиксации быстропротекающих процессов с низкими интенсивностями излучения различной природы, является одной из актуальных задач оптики и физики конденсированного состояния вещества. Еще большую актуальность эта проблема приобретает в случаях, когда требуется регистрация процессов, сопровождающихся сразу несколькими видами излучения. Ярким примером таких процессов являются протекающие в холодной неравновесной плазме (ХНП), образующейся, например, в виде электронных лавин при пробое газа в узком разрядном промежутке микронной толщины между электродами Роговского, один из которых или два покрыты диэлектриком. Знания протекающих процессов в описанных условиях представляют большой интерес, прежде всего в научной и прикладной фотографии для разработки теории газоразрядного фотографического процесса и при создании специальных фотоматериалов для дифференцированного анализа оптической и газоразрядной информации; технике высоких напряжений при оценке срока службы диэлектрической изоляции; газоразрядном фотографировании (ГРФ) различных объектов, включая и биологические с целью, например, медицинской диагностики и терапии (например, д?арсонвализация); газовой электрохимии, где слаботочный газовый разряд (ГР) лавинной формы используется, в частности, для озонирования воздуха и увеличения адгезионной способности поверхности материалов, наконец, в электронной технике при конструировании, например, газоразрядных визуализаторов.

Практика показала, что удовлетворяющими вышеперечисленным требованиям средами являются фотослои на микрокристаллах (МК) галоидного серебра (AgHal), позволяющие фиксировать распределение электронных лавин ГР по площади разрядного промежутка, а затем по фотоизображению изучать их. Как правило, при ГРФ процессов, протекающих в данных условиях, фотоматериал сам выступает диэлектриком, покрывающим электрод и непосредственно подвергается воздействию ионизованного газа и сопровождающего его светового и других излучений. Несмотря на простоту способа фотографической регистрации газоразрядных процессов его использование для данных целей пока ограничено из-за невозможности расшифровки зафиксированной фотоносителем информации вследствие отсутствия знаний о процессах и механизмах ее фиксации, то есть, процессах взаимодействия слаботочного лавинного ГР с МК AgHal.

В настоящей работе была поставлена цель: исследовать процессы взаимодействия холодной неравновесной плазмы, образующейся при горении слаботочного лавинного газового разряда с галогенсеребряной фотоэмульсией, установить закономерности их протекания, разработать феноменологическую физико-математическую модель этих процессов с последующей ее экспериментальной апробацией, оценить информационные возможности галогенсеребряных фотоматериалов при газоразрядном экспонировании и на основе полученных результатов разработать технические устройства для нужд науки, техники, производства, сельского хозяйства, экологии, медицины и биологии.

Для достижения поставленной цели требовалось решить следующие задачи:

1. Исследовать физические закономерности развития лавинного ГР при одноимпульсном режиме его возбуждения в воздухе атмосферного давления и узком разрядном промежутке микронной толщины между электродами Роговского (однородное электрическое поле), один из которых покрыт галогенсеребряным фотоматериалом (являющимся многослойным диэлектриком). При этом для микросекундных видеоимпульсов высокого напряжения положительной и отрицательной полярности определить основные параметры разряда: время его запаздывания относительно переднего фронта импульса и время горения; напряжения зажигания и погасания, интегральный ток, а так же, по газоразрядным сенситограммам на фотоматериалах, охватываемую площадь. Используя измеренные параметры ГР вывести математическую формулу и оценить по ней экспозиционные дозы воздействия разряда на галогенсеребряный фотоматериал и объект визуализации.

2. Разработать методику регистрации интегральных спектров для однородного электромагнитного излучения энергетической плотностью ?10^-6 Дж/м² и длительностью ?10^-6 с в ближнем ультрафиолетовом и видимом диапазонах и с ее помощью при разно-полярных видеоимпульсах высокого напряжения исследовать спектр излучения лавинного ГР, возбуждаемого в выше описанных условиях.

3. На основании экспериментальных результатов по физике импульсного пробоя воздуха атмосферного давления в микронном разрядном промежутке и знаний об электронных и электронно-оптических свойствах кристаллов AgHal, разработать феноменологическую физико-математическую модель процессов взаимодействия слаботочного лавинного разряда с фотоэмульсионными МК AgHal при импульсах положительной и отрицательной полярности.

4. При разно-полярных видеоимпульсах определить ответную реакцию галогенсеребряных фотоматериалов на газоразрядное воздействие и вывести математическую формулу для оценки их газоразрядной чувствительности (ГРЧ), а так же, исследовать влияние импульсного, однородного электрического поля высокой напряженности на газоразрядный фотопроцесс.

5. Путем топографического разделения скрытого газоразрядного изображения (СГРИ) на глубинную и поверхностную составляющие, исследовать при импульсах положительной и отрицательной полярности механизм взаимодействия слаботочного лавинного ГР с фотоэмульсионными МК AgHal стандартных и специально синтезированных фотоэмульсий, содержащих в кристаллах различное количество поверхностных и глубинных электронных ловушек с различной эффективностью.

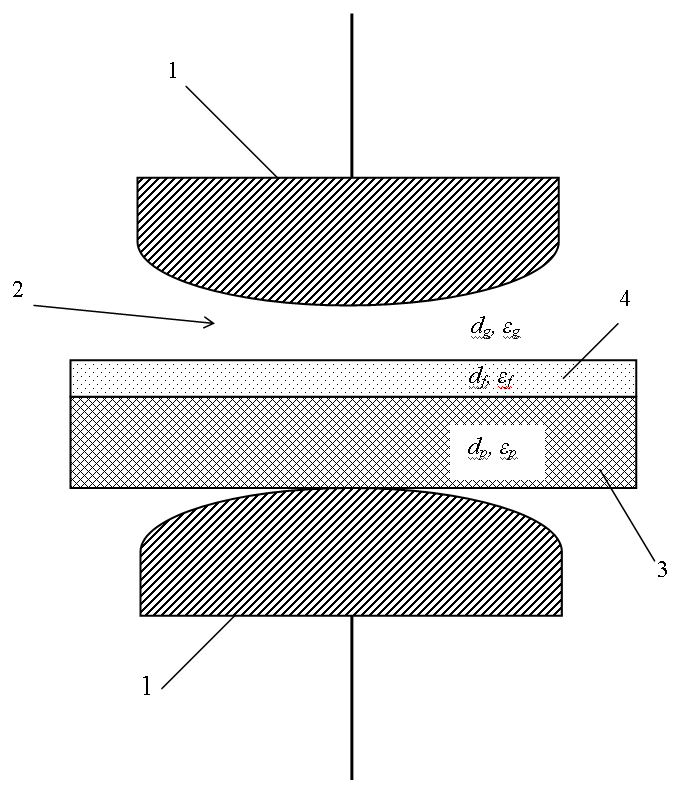
Краткое описание заменяемого процесса или решаемой проблемы

Как следует из работ отечественных и зарубежных авторов и наших наблюдений, вся совокупность процессов ГРФ может быть представлена в виде трех основных стадий.

1. Стадии предшествующей ионизационным процессам в газе: формирование в разрядном промежутке электромагнитного поля высокой напряженности и определенной геометрии, зависящих от величины приложенного напряжения, формы электродов и состояния их поверхностей; электро-геометрических характеристик регистрирующего материала (устройства и пр.), расположенного на одном из них (или обеих электродах), а так же, от электрической природы и геометрической формы других объектов, помещенных в этот промежуток.

2. Движение частиц ионизованного газа в электромагнитном поле, сформированного в разрядном промежутке (согласно условиям, перечисленным в п.1), то есть, сам ГР, «несущий» изображение (информацию).

3. Изменение состояния регистрирующей среды под действием частиц ионизованного газа, то есть, процесс фиксации газоразрядной информации и взаимодействие ионизованного газа с объектом (ами) фотографирования.

Постадийно рассмотрим эти процессы (без учета влияния объекта фотографирования).

В рассмотрении данного вопроса нас будут интересовать:

1. Распределение напряженности однородного электрического поля в трехслойном конденсаторе, образованного фотоматериалом и газовым слоем между электродами (рис. 1). Здесь 1 – электроды Роговского или Феличи; 2 – газоразрядный промежуток; 3 – диэлектрическая подложка фотоматериала; 4 – его фотоэмульсионный слой.

Рис. 1. Схема газоразрядной установки для фоторегистрации лавинного разряда. Обозначения в тексте

2. Влияние электро-геометрических характеристик галогенсеребряной фотоэмульсии на формирование электрического поля в газоразрядном промежутке.

При приложении внешнего, однородного электрического поля к трехслойному конденсатору, его напряженность распределится между слоями конденсатора, согласно, их электро-геометрических характеристик: толщины d и диэлектрической проницаемости ?:

Е_g = Е (d_g+d_f+d_p) / ?_g(d_f/?_f + d_p/?_p),                                 (1)

Е_f = Е (d_g+d_f+d_p) / ?_f(d_g/?_g + d_p/?_p),                                 (2)

Е_p = Е (d_g+d_f+d_p) / ?_p(d_g/?_g + d_f/?_f),                                 (3)

где Е_g, Е_f, Е_p – напряженности поля в газовом, фотоэмульсионном слоях и подложке, соответственно; d_g, ?_g; d_f, ?_f; d_p, ?_p– толщины и диэлектрические проницаемости этих слоев; Е– средняя величина напряженности поля в конденсаторе

Е = U/ (d_g/?_g + d_f/?_f + d_p/?_p),                                     (4)

где U – напряжение на обкладках конденсатора.

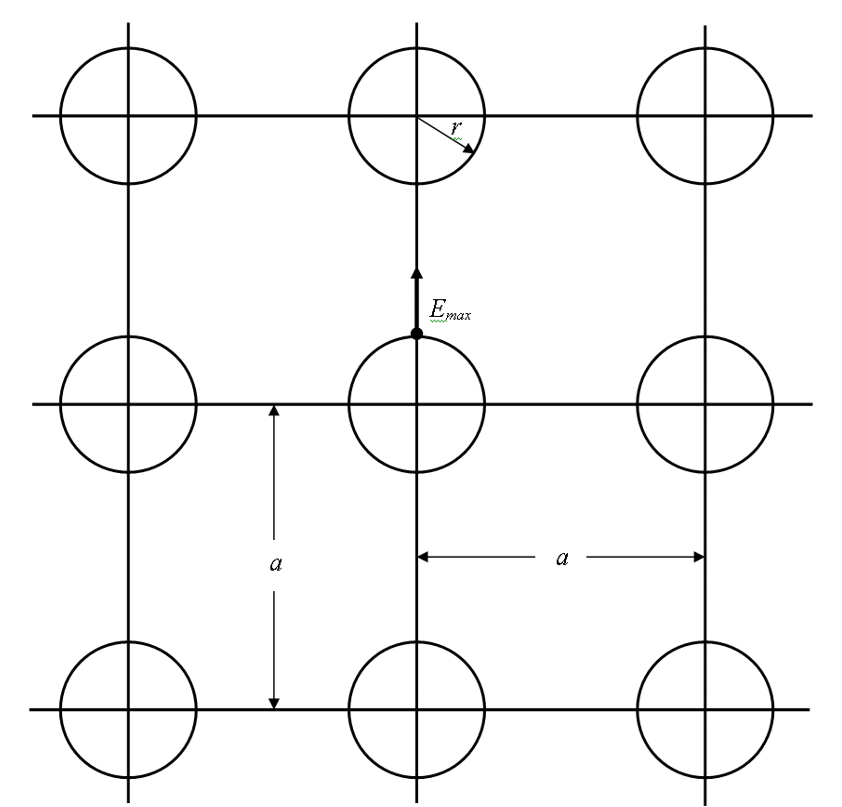
Рис. 2. Упрощенная модель фотоэмульсионного слоя. Обозначения в тексте

Рассматривая вопрос о распределении напряженности электрического поля в галогенсеребряном фотоматериале, мы представляли его фотоэмульсионный слой однородной и изотропной средой. Поэтому для такого фотоматериала формулы 1 – 4 справедливы. Реально же, фотослой – это гетерогенная смесь желатины с распределенными в ней МК AgHal и сильно различающимися между собой электрическими характеристиками. Так, для желатины ?_G= 3, а для AgHal – ?_AgHal ~ 13. Такое различие должно приводить к существенной неоднородности поля в фотослое. Оценивая эту неоднородность, сразу отметим, что точный ее расчет у поверхности кристаллов весьма сложен, даже если они будут иметь форму шариков одинакового радиуса и притом однородно распределенных в желатине. Поэтому ограничимся лишь приближенными оценками.

На рис. 2 представлена упрощенная модель фотоэмульсионного слоя. Здесь r – радиус кристаллов, а – расстояние между их осями. Если r << a, то используя работу Рэлея, можно определить максимальную напряженность электрического поля Е_mаxнад сферическим включением. Для этого введем концентрацию сфер ? = 4?r³/3a³ и, воспользовавшись, определим коэффициент неоднородности поля k_s, вносимой сферами.

k_s= Е_max/Е = 3f / (? +2+(1- ?)f),                                   (5)

где f = ?_AgHal /?_G. Расчет показывает, что для МК AgBr, размерами порядка микрона и расстоянии между ними ~10 мкм при f= 4,3, величина k_s = 2,05. При k_s с такой величиной поле является сильно неоднородным.

Еще раз подчеркнем, что рассчитанная величина k_sсправедлива только при r << a и ? << 1. В реальных же фотоэмульсиях, как правило, r ? a. Об этом свидетельствуют электронно-микроскопические фотографии фотоэмульсионных кристаллов, представленных на рис. 3.

Рис. 3. Электронно-микроскопические изображения МК AgHal безаммиачной (а) и аммиачной (б) эмульсий, полученных одноструйным

методом; кубической (в) и таблитчатой (г), полученных методом двухструйной эмульгации

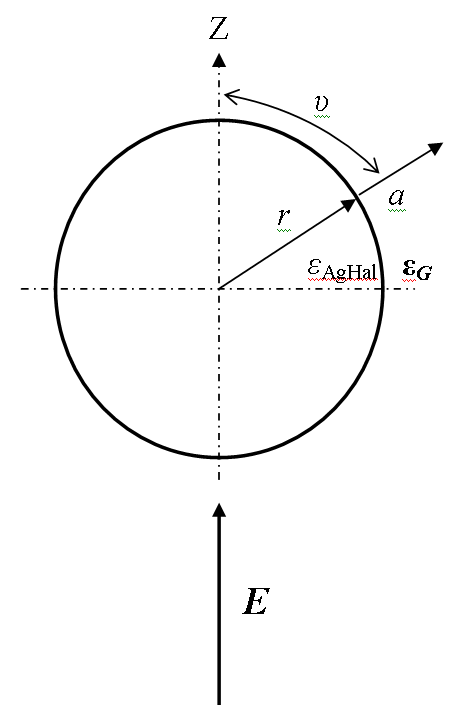
Рис. 4. Система координат для оценки искажения электрического поля МК AgHal в фотослое

До настоящего времени задача определения Е_maxв системе, показанной на рис. 2, как функция от Е, r, a, ?_G, ?_AgHal при любых соотношениях между r и aне решена. Поэтому такая задача решалась качественно для случая внешнего, неоднородного электрического поля. Воспользовавшись известными выражениями Пуассона решим эту задачу для внешнего, однородного поля.

Оценим расстояние, на котором неоднородность поля, созданная одним кристалликом, будет заметна в том месте, где находится другой. Для этого рассмотрим отдельный МК AgHal той же геометрии (рис. 4) с диэлектрической проницаемостью ?_AgHal = 13 и радиусом r, находящегося в желатине с ?_G= 3. Введя полярную систему координат допустим, что кристалл находится в однородном поле Е с divE = =0, которое направлено вдоль полярной оси Z, а его центр совпадает с центром координат. Тогда в указанных координатах в отсутствие сферы потенциал имеет вид

? = – E_oacos?,                                               (6)

где E_o – напряженность поля в точке а = 0. Поскольку потенциал сферы должен быть конечным, то при а < rищем решение в виде

?₁ = – В acos?,                                              (7)

а вне сферы ищем решение в виде суперпозиции начального поля и возмущения, внесенного сферой:

?₂ = – E_oa cos ? + А cos ?/а²,                       (8)

где А и В не зависят от а.

Из полученных формул видно, что неоднородность поля, вносимая кристалликом зависит не только от а, но и от полярного угла ?. Поэтому нам необходимо искать характеристику этой неоднородности, усредненную по углам. За меру неоднородности примем безразмерный параметр:

,      (9)

характеризующий, насколько в среднем изменяется E² на отрезке r₁, равном радиусу кристаллика r, находящегося на расстоянии а от его центра. Этот параметр сопоставим с другим безразмерным параметром:

,         (10)

найденного по формуле (9), и характеризующего изменение квадрата поля на поверхности МК, вызванное самим этим кристалликом. Положим, что взаимное влияние кристалликов начинает сказываться при F = 0,1P, то получится следующее уравнение 14 степени относительно g=r/a:

,           (11)

Численное решение этого уравнения при f = 4,3 и r₁ = r дает a ? 1,9r. Это значит, что, если поверхность второго кристаллика находится на таком расстоянии от центра первого, то на ней уже начинает сказываться искажающее влияние электростатического поля первого кристаллика. Ясно, что центр второго кристаллика может находиться при этом на расстоянии 2,9rот центра первого. Тогда, для МК, например, размером ~1мкм взаимовлияние начнется при a = 0,95мкм, то есть, на расстоянии между кристалликами, соизмеримом с их размерами или меньше его. Из сказанного следует, что при сближении МК, вплоть до их контакта, радиус проявления неоднородности поля, создаваемого одним кристалликом будет уменьшаться, компенсируясь, полем другого. Однако, из-за большой разницы значений ? МК AgHal и желатины, на границе их раздела, неоднородность поля сохранится. В итоге, это с одной стороны должно приводить к уменьшению неоднородности поля в газовом промежутке, граничащем с фотослоем, с другой – к увеличению ?_f   и объемной концентрации С_V МК в нем.

Так как фотоэмульсия может быть представлена матричной системой, то для расчета параметра ?_f будет справедливо выражение:

,      (12)

Обычно С_Vв фотоэмульсиях колеблется от 0,08 до 0,4, тогда ?_f  ~  4,0 – 8,0.

С появлением первичного электрона, разогнанного полем, в газоразрядном промежутке начинаются ионизационные процессы с образованием электронных лавин ГР. Как было отмечено выше, наличие диэлектрика на электроде придает особенность этим процессам, принципиально отличающим их от процессов пробоя газа между металлическими электродами, в частности, увеличивая «время жизни» лавин, не давая перейти в иную форму разряда – стримерную. Поэтому здесь целесообразно рассматривать газоразрядные процессы в двух случаях: протекающие в объеме промежутка и на поверхности фотослоя, граничащего с газовым.

Основной теорией электрического пробоя газа в физике ГР является развитая в 1901 году Таунсендом, рассматривающая разряд при небольших давлениях и разрядных промежутках как движение электронных лавин, воспроизводящихся за счет электронно-ионной эмиссии на катоде. Однако, как показывают многочисленные исследования по пробою газа атмосферного давления, теория Таунсенда в таких условиях «не работает». Так, например, было обнаружено, что время формирования разряда в газе атмосферного давления примерно на два порядка меньше предсказываемого ей, указывая на течение иных физических процессов, особенно, когда они происходят на импульсах и между электродами, один из которых покрыт диэлектриком. Поэтому в настоящее время существуют альтернативные теории.

При импульсном пробое газа между моментом приложения напряжения к промежутку и началом пробоя, которое обычно фиксируется по резкому спаду напряжения, проходит некоторое время, называемое временем запаздывания t_zp. В свою очередь t_zpразбивают на две составляющие: статистическое время запаздывания t_s, в течение которого в промежутке появится инициирующий разряд электрон, и время формирования t_f, в течение которого, за счет развития первичной электронной лавины и последующих стадий нарастания ионизации, развивается ГР. Ясно, что в зависимости от условий в предпробивной стадии соотношение между t_s и t_fможет быть различным. Величина t_s коренным образом зависит от условий появления в промежутке первичных электронов n₀, освобождаемых с катода в единицу времени и вероятности того, что каждый из них может вызвать лавину:

t_s= 1/ Р • n₀ = e / Р • i,                                             (13)

где e – заряд электрона, i – ток эмитируемых с катода электронов, Р – вероятность ионизации газа этими электронами, определяемая по с учетом эффекта Шотки как

Р = X ехр (–В(Ф – ?)/2еl_е Е).                                  (14)

Здесь X = 1 – ехр (– d_g/l_е) – вероятность соударения электрона с молекулой газа (в рассматриваемых условиях обычно равная единице); l_е – длина свободного пробега электрона в газе (определяемая как l_е = 1/Q, где Q – эффективное сечение ионизации газа электронным ударом); ? = (е³Е/4??₀)^1/2; ?₀ – диэлектрическая постоянная вакуума; Ф – энергия ионизации молекулы (атома) в отсутствие электрического поля; В – безразмерный коэффициент, постоянный для данного химического состава газа.

Динамика развития электронных лавин может быть описана следующей системой уравнений:

?n_е/?t + divn_е (eE/m?_e – n_еT_e/m?_en_е) = ?_in_е = ?n_i/?t;

?_e? – ??_eT_e – ?_i(T_e + Ф) = 0;                                   (15)

div E = 4?e (n_е– n_i).

Здесь ? = е²Е²/m?_e² – энергия набираемая электроном в электрическом поле Е=Е_v+ Е_R (где Е_v – напряженность внешнего поля, а Е_R – поле разделения зарядов лавины); ? ? 2m?_e/М – доля упругих потерь при электронно-атомных столкновениях; М – масса атома (молекулы) газа;?_eи ?_i– частоты ионизационных столкновений электронов и ионов, где (в борновском приближении, при учете максвелловского распределения электронов по скоростям с температурой Т_е)

?_e= 4N₀?₀ (Т_е)^1/2 / (2?m)^1/2,                                     (16)

?_i = (4?₀N₀ / (2?mТ_е)^1/2) exp (– Ф/Т_е),                    (17)

N₀ – плотность нейтральных атомов, m – масса электрона, ?₀ и ?₀ – некоторые константы, причем в борновском приближении ?₀Z* = 2?₀Ф, где Z* – эффективное зарядовое число ионов (для простоты считается Z* = 1), а ?₀ – сечение рассеяния электронов атомами при малых энергиях.

При анализе системы уравнений (15) подчеркнем, что нас будет интересовать процесс развития лавины до перехода в стример, пока Е₀<< Е_R. Для этого составим уравнение теплового баланса, положив ? = ?₀ = е²Е²/m?_e² и записав его в виде

?е²Е₀²/8N₀²?₀² = ?T_e² + ?₀/?₀ ехр (– I/T_e) (Ф + T_e).       (18)

Уравнение (18) определяет постоянную электронную температуру в лавине Т_е = f(E₀/N₀).

На начальной стадии развития лавины, пока ее поперечный размер – радиус лавины r_L мал по сравнению с дебаевским радиусом, ее расширение будет определятся диффузией электронов, так как

еЕ_R ~ 4?е²n_еr_L << T_e/r_L.                                        (19)

В результате из (15) находим электронную плотность в лавине

n_е (r, t) = (4?Dt)^-3/2exp[?_it– (?² + (z – ut)²/4Dt].   (20)

Здесь u = еЕ₀/m?_e – скорость дрейфа электронов в поле Е₀, направленная вдоль оси Оz, а D = u²T_e/?_e– коэффициент электронной диффузии, t– время диффузионного процесса, ?² = х² + у².

Из выражения (20) следует, что в лавине электроны дрейфуют вдоль поля с постоянной скоростью u, которая по величине согласно (20), всегда меньше их тепловой скорости. В поперечном направлении лавина расширяется благодаря электронной диффузии, причем радиус ее головки равен

r_L= (6Dt)^1/2 = (6Dz /u)^1/2,                                        (21)

где z = ut.

Детальное рассмотрение процесса ионизации газа первичными электронами показало, что он не происходит при непосредственном электронном ударе, а зависит от ионизирующей способности фотонов, излучаемых возбужденными от этих электронов атомами или молекулами газа. Причем фотоны должны быть резонансными к молекулам (атомам) данного газа.

Впервые существование фотоионизирующего излучения, испускаемого электронной лавиной, было экспериментально обнаружено Ретером в камере Вильсона. В процессе исследований выяснилось, что коэффициент поглощения ? для различных газов оказывается, в пересчете на атмосферное давление, порядка ~ 1 см^-1. Так в воздухе ? ? 1,8 см^-1, в О₂ ? ? 1 см^-1, в Н₂ ? ? 0,8 см^-1 и т.д. Хотя опыты Ретера и других исследователей убедительно доказали существование ионизирующего излучения, образуемого электронной лавиной, механизм фотоионизации газа долгое время оставался неясным и, в какой-то мере, противоречивым. Дело в том, что при анализе ионизационных процессов в однородных газах, а так же их смесях, не оказывалось таких электронов, которые могли бы привести к образованию фотонов с энергией, превышающей энергию ионизации атомов или молекул ионизируемого газа, и в то же время способных при малом времени развития разряда (~10^-7с) обеспечить его распространение на большие расстояния, то есть, быстро охватить весь объем промежутка.

Для разрешения этого противоречия была высказана гипотеза о возможности излучения возбужденными атомами (или молекулами) газа за счет электронного удара, резонансных фотонов. Последовательность этих процессов можно представить в виде следующих уравнений:

а) возбуждение атома (но, не ионизация!) электронным ударом

А + е > А* + е;                                                (22)

б) эмиссия света возбужденными атомами

А* > А + h?.                                                   (23)

Наряду с этими процессами могут происходить ионно-молекулярные химические реакции ассоциативной ионизации по схеме

А* + В > (АВ)⁺ + е^–,                                      (24)

где А и В – нейтральные атомы, А* - возбужденный атом (молекула).

Так, например, для ионизованного воздуха основную роль играют реакции с участием кислорода

О₂* + N₂ > NO + NO⁺ + е^–                                 (25)

O₂* + O₂ > O₃ + O + е^–.                                (26)

В тоже время аналогичные реакции с возбужденным азотом для образования дальнопролетных фотонов в воздухе не играют существенной роли, так как резонансные фотоны, отклонившиеся от основной частоты, будут поглощаться кислородом в самой лавине.

Поскольку в указанных реакциях возникают резонансные фотоны, то они способны поглощаться молекулами того же газа, так как коэффициент поглощения для него может оказаться очень большим ? ? 10⁶ см^-1. Следовательно, такие фотоны практически не будут выходить из объема лавины. Однако некоторая их часть, благодаря конечной ширине спектральной линии, может «выйти из резонанса» – сильно отклонится от основной частоты, и такие фотоны будут способны пролететь большие расстояния до своего поглощения. Если этот процесс происходит в смеси газов, то фотоны могут оказаться резонансными для атомов (молекул) другого газа и вызвать их возбуждение или ионизацию. Так, например, для воздуха фотоны с энергией 12,2эВ, образующиеся при излучении азота, являются резонансными как к нему самому, так и кислороду, способные его ионизировать. Об энергетической возможности протекания этих процессов, говорят данные таблицы 1, в которой представлены значения минимальных энергий возбуждения и ионизации некоторых газов.

Таблица 1 Минимальные энергии возбуждения и ионизации некоторых газов

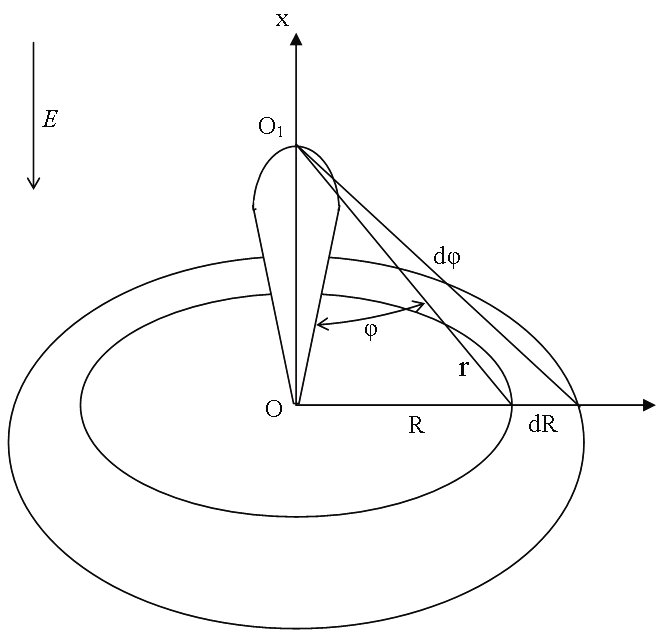
Произведем количественные оценки описанных процессов для случая лавинного ГРФ. Рассмотрим промежуток толщиной d_gс плоскими электродами, бесконечными в поперечном направлении (рис. 5). При этом ось х направлена вдоль поля Е. Пусть из точки О стартовала лавина, проходящая путь dх за время dt. Положим, что из точки О₁ испустился фотон частоты ?.

Рис. 5. Схема к расчету излучения резонансных фотонов, испускаемых электронной лавиной ГР. Обозначения в тексте

Тогда, если бы спектральная линия была бы бесконечно тонкой, вероятность для фотона пролететь расстояние r без поглощения была бы равна

Р(r) = exp (– ?r).                                                               (27)

С учетом конечной ширины спектральной линии эта вероятность определится соотношением:

, (28)

Здесь Р(?) – форма спектральной линии; ?(?) – зависящий от частоты коэффициент поглощения фотонов.

Оценки показывают, что в газе при нормальных условиях уширение спектральной линии происходит в основном за счет соударения молекул. Поэтому в качестве формы спектральной линии можно выбрать ударную лоренцовскую. Откуда имеем 

Р(?) = (Г/2?)/(? + ?₀)² + (Г²/4),                                        (29)

где Г = N?_m?_ef  – ударная ширина спектральной линии; ?_ef– эффективное сечение столкновения молекул газа; N и ?_m– их концентрация и скорость теплового движения. При этом

?(?) = (?₀ Г²/4) / (? – ?₀)² + (Г²/4),                                 (30)

где ?₀ – коэффициент поглощения фотона частоты ?₀ в центре линии. Подставляя (30) и (29) в (27), производя интегрирование и учитывая, что ?₀r>> 1, получим

Р(r) = 1/(??₀r)^1/2.                                                                 (31)

Краткое описание предлагаемого технологического процесса

В результате проведенной научно-исследовательской работы было разработано новое техническое устройство – «ФОТОАППАРАТ ГАЗОРАЗРЯДНЫЙ» (ФГР), (со специальными приставками для газоразрядной визуализации и фотографирования в атмосфере различных газов или их смесей гранулированных и жидкофазных биообъектов, участков тела человека и животных). В работе показано, что разработанный прибор позволяют экспрессно и дифференцированно проводить информационный анализ конкретных органов или систем организма, открывая перспективы выявления конкретных заболеваний и осуществлять спектроскопию однородного низко-интенсивного электромагнитного излучения (менее 10^-6Дж/м²) в диапазоне 260 – 750 нм включая конкретно выбранные участки исследуемых объектов. Заложены основы новых научных направлений: «Газоразрядные способы извлечения информации из окружающей материи» и «Газоразрядная обработка различных материалов», что открывает большие перспективы использования ХНП как нового и универсального переносчика информации (в отличие от электромагнитных, акустических волн и др.) и как средства воздействия на различные объекты и материалы с целью придания им уникальных физико-химических свойств и характеристик, что имеет как научное, так и практическое значение для биологии, медицины, ветеринарии, сельского хозяйства, экологии, криминалистики, технической диагностики и неразрушающего контроля при дефектоскопии или дефектометрии.

Перечисленные возможности достигаются универсальностью свойств ХНП, существование которой сопровождается широтой спектров как акустических, так и электромагнитных колебаний, формированием в ее окрестности электрического и магнитного полей различной напряженности и геометрии, а также образованием продуктов горения, не достижимых при обычном химическом синтезе, возможностью регистрации этих спектров регистрирующей средой на основе галогенидов серебра и преобразованием этих изображений в оптический диапазон, обеспечивая удобство их визуального и (или) технического анализа.

На основе теоретического и экспериментального анализа вышеперечисленных возможностей ХНП показаны перспективы внедрения ХНП-методов. 

1. В медицине – это один из перспективных и безлучевых методов диагностики конкретных заболеваний, а так же, энергосберегающих и экономически выгодных, позволяющих сэкономить более четырехсот тысяч рублей в год.

2. В сельском хозяйстве – это незаменимое и экспрессное средство оценки морозоустойчивости растений, а также предпосевной обработки семенного материала различных сельхозкультур для увеличения их урожайности более чем на 15%.

3. В криминалистике – это средство, например, выявления экономических преступлений: подделки ценных бумаг, документов, денежных купюр и пр., что достигается физической природой ХНП – «видеть» не только оптическую составляющую исследуемого документа, но и одновременно их механические, электрические и геометрические свойства. Теже возможности могут быть достигнуты лишь при использовании отдельного устройства для выявления только какой-то одной характеристики. Поэтому ХНП здесь выступает качественно иным и универсальным переносчиком информации, что делает ее незаменимым и перспективным средством технико-криминалистического исследования.

4. В технической диагностике и неразрушающем контроле при дефектоскопии и дефектометрии различных дефектов, инородных включений, химической коррозии в деталях и узлах (особенно труднодоступных) машин, лопастей турбин и обшивке самолетов, металлических фермах мостов и др. обычно скрытых под слоями всевозможных покрытий (например, лакокрасочных). А возможность легкой автоматизации ХНП-устройств и их малые габариты, а также вес и стоимость, делают их незаменимым и экономически выгодным средством экспрессного неразрушающего контроля и технической диагностики практически любой техники и технического сооружения, позволяя быстро и легко внедрить их на территории Краснодарского края и за его пределами.

5. В охране окружающей среды и экологии – это принципиально новое средство очистки и обеззараживания сточных вод, полив которой сельскохозяйственных угодий увеличивает физиологические показатели роста и развития семян и соответственно ведет к повышению их урожайности.

Основные технические характеристики нового разработанного прибора

ФОТОАППАРАТ ГАЗОРАЗРЯДНЫЙ

Технико-экономическое обоснование применения инновационной технологии

Технико-экономические показатели трудо-энерго-природосбережения нового процесса

Экономический эффект (за один год) с учетом стоимости изделия, руб. - В сравнении с «Корона-ток»:  131179,82.

Работа прибора не сопровождается выбросом каких-либо вредных веществ, а по факту зажигания газового разряда в воздухе, даже обогащает его озоном, что дополнительно является полезным фактором для здоровья (озонирование воздуха).

Новые потребительские свойства продукции

- снижение металлоемкости;
- уменьшены габариты;
- повышена достоверность и емкость получаемой информации.
Последнее, обеспечивается за счет разделения полярностей высоковольт-ных импульсов, возбуждающих газовый разряд и возможности регистрации у биообъектов вызванных разрядом биопотенциалов.

Качественные характеристики, предъявляемые к сырью и материалам

Продукция соответствует государственным стандартам.

Стадия и уровень разработки

Разработанное устройство прошло экспертизу на соответствие возможности использования в медико-биологической практике и признаны безопасными для здоровья и жизни людей.
В настоящее время имеются действующие опытные образцы прибора с отработанной методикой его эксплуатации, готового для промышленного производ-ства.

Предлагаемые инвестиции

6 млн. руб.

Рынки сбыта

Потенциальными потребители продукции могут являться: медицинские, ве-теринарные и сельскохозяйственные учреждения и научно-исследовательские центры, органы службы безопасности, правоохранительные органы, органы су-дебно-медицинской и судебно-технической экспертизы, авто- и железнодорож-ные службы, службы технической диагностики и неразрушающего контроля изделий и конструкций авиационно-космических, радиоэлектронных, оборон-ных, нефтехимических, жилищно-эксплуатационных и строительных предпри-ятий, а также экологических служб и служб охраны природы, как Российской Федерации, так и организации перечисленных профилей иностранных госу-дарств.

Возможность и эффективность импортозамещения

Предлагаемая в проекте разработка не имеют аналогов на мировом рынке аналогичной продукции.

Возможность выхода на мировой рынок

Срок окупаемости (в месяцах)

24

Дата поступления материала

25.10.2006