ПОДРОБНАЯ ИНФОРМАЦИЯ
Заявку на получение дополнительной информации по этому проекту можно заполнить здесь.
|
Номер 24-121-03 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Наименование проекта Алгоритм маркетингового обоснования оптимальных параметров сельскохозяйственной техники на стадии проектирования |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Назначение Повышение качества проектируемой сельскохозяйственной машины и ее конкурентоспособности. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рекомендуемая область применения Экономическое обоснование параметров проектируемой сельскохозяйственной техники. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Описание
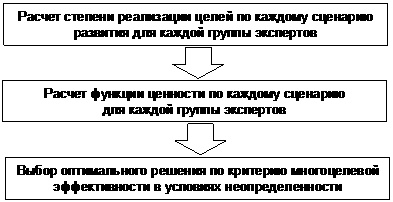
Результат выполнения научно-исследовательской работы. Предлагаемая методика расчета состоит из двух этапов: статистического и маркетингового. На первом этапе происходит создание информационной базы за счет сбора необходимых данных путем опроса экспертов по методу Дельфи в несколько туров. На втором этапе определяются оптимальные параметры машины исходя из максимального значения функции ценности. Схематично данный этап изображен в виде крупных расчетных блоков.
В этой части методики используется метод многоцелевой оптимизации с момента определения степени реализации поставленных целей. При решении задачи по подбору оптимального сочетания параметров новой техники цели определены назначением методики и в общем виде сводятся к максимизации многоцелевого комплексного показателя. В качестве критериев принимаются показатели из инженерных моделей оптимизации. Относительные важности этих критериев определяются на первом (статистическом) этапе. Для расчета степени реализации цели для каждого критерия необходимо учесть все сочетания факторов, влияющих на критерий. С помощью моделей регрессии, полученных разработчиками машины, можно просчитать все критерии оптимизации. Для того, чтобы отсеять схемы с неправильными и неэффективными критериями, необходимо ввести ограничения вида
гдеy il- абсолютное значениеi-го критерия оптимизации приl-ой схеме сочетания факторов; y iminиy imax- соответственно минимальное и максимальное значенияi-го критерия оптимизации.
Относительные оценкиe ilрассчитываются дляi-го критерия оптимизации поl-ой схеме, удовлетворяющей ограничениям вида (1). Их значение зависит от выбора формул расчета. Для критериев оптимизации, которые в принципе могут принимать нулевые значения, производят расчет по методу
Если достижение нулевого значения рассматриваемого критерия оптимизации практически не осуществимо и невозможно даже в идеале (
Если зависимость Если для расчета функции ценности использовать линейную свертку, то в общем виде дляj-го сценарияk-ой группы экспертов приl-ой схеме сочетания факторов она будет выглядеть следующим образом
где Результаты расчетов по формулам (2 - 6) заносятся в таблицу. После определения показателей многоцелевой эффективности (функции ценности) необходимо выбрать оптимальную схему сочетания факторов с наибольшимe jkопт. В общем виде модель оптимизации с учетом ограничений выглядит
Для устранения фактора неопределенности используются элементы теории игр. При принятии наиболее осторожной стратегии следует воспользоваться критерием максимина
Если при обработке анкетного вопроса о вероятностях наступления сценариев развития наблюдается высокий уровень согласованности экспертов, можно принимать решения с помощью критерия Байеса-Лапласа, результаты скорректированных по сценариям показателей многоцелевой эффективности сводятся в таблицу.
гдеp jk- вероятность наступленияj-го сценария вk-ой группе экспертов.
Матрица расчета скорректированной функции ценности в условиях неопределенности
Если при обработке анкетных данных согласие достигается во всей совокупности экспертов, то достаточно рассчитать функции ценности только для общей группы. Если согласие экспертов в общей совокупности не достигается или незначительно, необходимо учитывать функции ценности по каждой группе. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Преимущества перед известными аналогами Используется многоцелевой подход, решение может приниматься в условиях неопределенности. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Стадия освоения Опробовано в условиях опытной эксплуатации |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Результаты испытаний Технология обеспечивает получение стабильных результатов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Технико-экономический эффект Снижение трудоемкости и повышение производительности труда в 2 раза. Улучшение качества изделий. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Возможность передачи за рубеж За рубеж не передаётся |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дата поступления материала 25.11.2003 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Инновации и люди

У павильонов Уральской выставки «ИННОВАЦИИ 2010» (г. Екатеринбург, 2010 г.)

Мероприятия на выставке "Инновации и инвестиции - 2008" (Югра, 2008 г.)

Открытие выставки "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)

Демонстрация разработок на выставке "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)
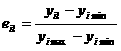 ; (2)
; (2)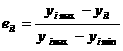 . (3)
. (3)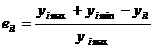 . (5)
. (5)