ИННОВАЦИИ БИЗНЕСУ

Результат выполнения НИР.

Оценка упругопластических напряжений и деформаций основана на методе перемещений, в котором используется однопараметрическая модель. В рамках данной модели при наличии единственной базисной функции , анализ полей перемещений и деформаций производится посредством кинематического параметра - обобщенного перемещения. В качестве базисной функции было взято упругое распределение деформаций вблизи сферической полости. При этом:

. (1)

Значение параметра нагружения соединения с порами при вычислении базисной функции принимали единичным , гдеg- модуль упругости второго рода.

Согласно механике сплошных сред силовые факторы в однопараметрической модели связаны следующим образом:

, (2)

где - внутренняя энергия сварного соединения на базисном поле деформаций и напряжений ;

v- объем деформирования;

- пластическая диссипация энергии при девиаторе неупругих деформаций ;

y- работа единичных внешних сил на базисном перемещении .

Задача сводилась к определению составляющих уравнения (2). Параметры иyопределяли на основе упругого решения. Для расчета при произвольной диаграмме деформирования использовалась структурная модель упругопластической среды. Согласно данной модели элементарный объем металла можно представить набором подэлементов, наделенных своими уникальными, идеально упругопластическими свойствами. Если диаграмму деформирования металла аппроксимировать некоторым количеством отрезков, характеризующих деформирование подэлементов, то для определения параметра сварного соединения в целом необходимо оценить данную величину для каждого из подэлементов и усреднить найденные значения. Для определения кинематического параметра уравнение (2) решали итерационным путем, используя при этом метод дополнительных напряжений. Этот метод может быть интерпретирован следующим образом. Наi-ой операции суммируются значение и некоторое приращение , величина которого определяет погрешность уравнения (2).

Как правило, для определения величины неупругих деформаций и напряжений используют способы, основанные на закономерностях перераспределения упругих напряжений и деформаций в пластических областях. Наиболее известным является метод Нейбера, позволяющий связать интенсивность напряжений и деформаций ( и ) в самой опасной точке конструкции при ее упругопластическом деформировании с соответствующими значениями интенсивности напряжений и деформаций в упругом теле ( и ). Из выражения:

, (3)

где и - коэффициенты концентрации интенсивности деформаций и напряжений в пластической области,

- коэффициент концентрации напряжений в упругой области,

следует, что

. (4)

То есть произведение интенсивности деформаций и напряжений - величина постоянная для данного концентратора.

Решая уравнение (4) совместно с диаграммой деформирования металла

, (5)

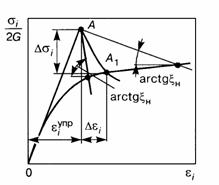
можно получить значения интенсивности неупругих деформаций вблизи контура пор.

На рисунке 1 показана процедура нахождения по известному упругому решению (точка А).

Рис. 1. Определение интенсивности деформаций в упругопластической стадии при нагружении соединений с порами

Для материалов с низкой степенью деформационного упрочнения и для острых концентраторов формула Нейбера дает завышенные значения местных напряжений и деформаций в упругопластической области. В связи с этим в правую часть формулы вводится поправочная функция . В рамках принятой модели получено аналитическое выражение для определения параметраx_н:

, (6)

где , - интенсивности полных и пластических деформаций в самой опасной точке.

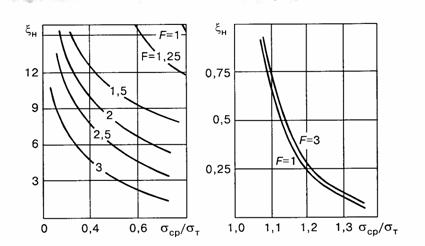
Графическая реализация результатов в виде зависимости параметраx_нот нагруженности сварного соединения , его геометрии и местоположения поры приведена на рисунке 2.

Рис. 2. Зависимость параметраx_нот величины внешних напряжений

Последние два параметра характеризуются поправочной функцией, которая находится путем сопоставления упругого решения для тел бесконечных и конечных размеров и решений в упругой стадии работы при различных положениях поры в швах. При локальном пластическом деформировании металла в окрестности порыx_нуменьшается с увеличениемf. В условиях общей текучести (рис. 2) влияниеfна критические напряжения незначительно.

Путь нахождения учитывает остроту концентратора, нагруженность соединения, его форму, местоположения поры, ее геометрические размеры.

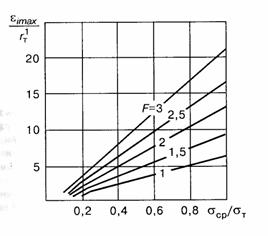
В зависимости от степени нагруженностиx_низменяется от 0 доҐ, что отражает реальное поведение соединения. При использовании формулы Нейбера параметрx_низменяется от 0 до 1, что не всегда соответствует действительности.

Для практического использования разработанной методики при определении нолей напряжений и деформаций построены графические зависимости (рис. 3 и 4). В случае, когда реализуется локальное пластическое течение вблизи контура поры, зависимость максимальной интенсивности деформации в опасной точке относительно нагрузки приведена на рисунке 3.

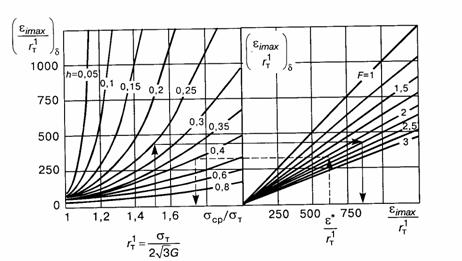
Рис. 4. Номограмма для определения максимальных упругопластических деформаций при и средних предельных напряжений для сварных соединений с порами

В качестве критерия разрушения использовалась критическая деформация, которую можно найти из диаграмм пластичности. Критическую нагрузку , соответствующую появлению в соединениях несплошностей на контуре пор, можно определить из соотношений:

; ; , (7)

где - функция, отражающая связь критической деформации с внешней нагрузкой ;

- функция обратнаяw.

Логика определения деформации в точке с максимальной интенсивностью напряжений в зависимости от степени нагружения, упрочняемости материала и поправочной функции показана на номограмме стрелками. Оценка критических напряжений , при которых происходят разрывы на контуре поры, представляет обратную задачу, ее решение показано на номограмме прерывистой линией.

Данный метод решения задачи по упругопластическому деформированию позволяет в каждом случае определить критическую интенсивность деформаций на контуре дефектов и соответствующий уровень средних предельных напряжений, при которых по периметру пор происходит образование надрывов.

Неблагоприятной ситуацией, способствующей образованию надрывов на контуре пор при низком уровне приложенных средних напряжений, является приближение дефектов к свободной поверхности на расстояние, меньшее двух диаметров пор.