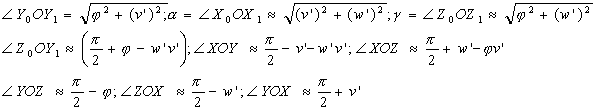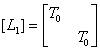ИННОВАЦИИ БИЗНЕСУ

Результат выполнения научно-исследовательской разработки.

При записи дифференциальных уравнений равновесия, необходимо учитывать изменение геометрии конструкции и положения в пространстве сечений под воздействием внешних сил. Традиционно принято уравнение равновесия в части, касающейся внутренних сил составлять относительно недеформированного состояния. Однако, пренебрежение фактом непоступательного смещения сечений в процессе деформирования может исказить фактическое равновесие системы.

Движение под нагрузкой исходного плоского сечения можно рассматривать как свободное движение твердого тела в общем случае. При этом полное перемещение сечения состоит из поступательного перемещения вместе с местной для этого сечения системой координат ox₁y₁z₁ относительно системы координат для всего стержня o₂x₂y₂z₂ и сферического движения сечения и закрепленной с ним дополнительной системы координат ox₀y₀z₀ относительно общего начала систем координат сечения, т.к. учет одинаковой депланации сечений, не нарушает существа гипотезы плоских сечений, что удобно использовать при конечно-разностном решении.

Местная система координат всего стержня o ₂x ₂y ₂z ₂ связана со стержнем в конструкции в недеформированном состоянии следующим образом: начало координат расположено в центре тяжести сечения, ось О ₂Х ₂ направлена либо по линии геометрических мест центров тяжестей (по исходной оси стержня), либо, для криволинейных стержней, по линии, соединяющей центры тяжестей крайних сечений. Оси o ₂y ₂ и О ₂z₂ образуют правую Декартову систему координат и могут быть ориентированы каким-либо произвольным способом (например, как главные оси инерции крайнего сечения).

Для каждого сечения положение системы координат ox ₁y ₁z ₁ следующее: начало координат расположено в центре тяжести сечения, ось ox ₁ направлена по касательной к линии геометрических мест центров тяжестей (к исходной оси стержня). Оси oy ₁ и oz ₁ образуют правую Декартову систему координат и могут быть ориентированы каким-либо произвольным способом (например, как главные оси инерции). Для прямолинейных стержней все оси системы координат ox ₁y ₁z ₁ параллельны осям системы o ₂x ₂y ₂z ₂.

Поступательная часть движения описывается тремя функциями u, v, w координаты Х ₂ движения точки О относительно системы координат o ₂x ₂y ₂z ₂ и характеризует отклонение точек деформированной оси от ее начального положения в направлении осей x ₂y ₂ и z ₂, соответственно. Вращательная часть движения характеризуется тремя углами поворотов j, w' , v' вокруг осей x ₁,y ₁ и z ₁ соответственно. Вращательную часть движения можно изобразить в виде трех поворотов на углы, подобные корабельным углам академика А.Н. Крылова. Это крутильный поворот сечения стержня и системы координат ox ₀y₀z ₀ вокруг оси ox ₁ на угол j; поворот сечения вокруг оси oz' ₁(новое положение оси oz ₁) на угол v', и поворот сечения и системы ОХ ₀У ₀z₀ вокруг оси ОУ ₀ (это новое положение оси ОУ ₁) на угол w'.

Уравнение равновесия внутренних и внешних сил стержня удобно составлять относительно местной системы координат o ₂x ₂y ₂z ₂. При этом целесообразно воспользоваться матрицей направляющих косинусов t0, характеризующей положение системы oxoyozo по отношению к системе ox ₁y ₁z ₁.

Углы между осями ОХ ₀ ОУ ₀, oz ₀ и осями ОХ ₁, oy₁, oz₁ выражаются через углы j, w' , v' из геометрических соображений с использованием для дуг окружностей единичных радиусов соотношений s = a • r = a и приближённой зависимости sin a»a. При этом получены следующие выражения для углов:

Таким образом, все девять углов между осями, а, следовательно, и девять элементов (косинусов) матрицы направляющие косинусов Т ₀ определены.

Запишем внутреннее усилие относительно координат ox₀y₀z₀ , затем с помощью матрицы направляющих косинусов преобразуем их к местной системе координат сечения ox₁y₁z₁, и (для криволинейных стержней) сделаем преобразование к местной системе координат стержня o₂x₂y₂z₂. Вектор внутренних усилий в сечении обозначим { f^j₀}

Преобразуем вектор внутренних усилий к местной, для данного стержня, системе координат ox₁y₁z₁:

где l_сф - матрица преобразования

Для составления уравнений равновесия внешних и внутренних сил в криволинейных стержнях сделаем переход к местной системе координат стержня:

Т ₁-матрица направляющих косинусов системы координат ox₁y₁z₁ по отношению к системе координат o₂x₂y₂z₂. Эта матрица определяется исходной геометрией стержня.

Обозначая вектор внешних усилий (с учетом деформированной схемы) к центру o { f ^e}, приходим к уравнениям равновесия вида:

Полная система уравнений равновесия стержня включает и условия равновесия всего стержня как твердого сдеформированного тела:

Таким образом, сформирована система уравнений равновесия внешних и внутренних усилий в стержне с учетом сферических движений нормальных сечений.

Объединение стержней в ансамбль элементов, конечно-разностная аппроксимация дифференциальных уравнений и замена интегрирования суммированием и дальнейший расчет производится по существующей методике

(Шеин А.И., Метод сечений аппроксимации элементов при расчете рамных каркасов. Известия вузов. Строительства. 2002, №3, с. 8-13)