ИННОВАЦИИ БИЗНЕСУ

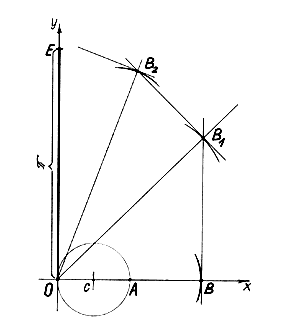
Результат выполнения технологической разработки.

Предложен совершенно оригинальный способ геометрического построения предельно точного отрезка численной величиной «p» с любой заданной степенью точности.

На рисунке показана схема таких построений. При этом последовательно выполняют по системе алгоритма несколько однотипных шагов, каждый из которых состоит всего лишь из 3 операций.

1. На координатной сетке ОХУ принимают отрезок ОА за величину диаметра заданной окружности с центром в точке С и откладывают на оси ОХ отрезок АВ, равный отрезку ОА.

2. Выполняют 1-ю операцию первого шага алгоритма: из точки О как из центра проводят циркулем дугу через точку В.

3. Выполняют 2-ю операцию первого шага: строят касательную к проведенной дуге в точке В и продлевают эту касательную вверх.

4. Выполняют 3-ю операцию первого шага: делят угол УОХ пополам биссектрисой, которая пересечет в точке В ₁ касательную из точки В.

Подобным же образом выполняют и следующие три операции второго шага алгоритма. При этом вновь проводят из точки О ₁ как из центра дугу уже через точку В ₁ и делят угол УОВ ₁ пополам, а затем строят касательную к дуге в точке В ₁ с целью нахождения точки В ₂ пересечения этой касательной с новой биссектрисой, делящей угол УОВ ₁ пополам.

Таким образом, сделав необходимое количество шагов алгоритма, достигают точку Е на вертикальной оси ОУ, когда отрезок ОЕ предельно точно будет равен длине заданной окружности с центром в точке С.

Что касается отношения длины окружности (в данном случае полученный отрезок ОЕ) к длине ее диаметра (в данном случае заданный отрезок ОА), то это отношение действительно абстрактно, когда отрезки ОА и ОЕ численно не определены в каких-либо принятых мерах длины.

Если отрезок ОА как заданная длина диаметра окружности, численно определен в какой-либо мере длины и составляет, например 1 м (и вообще 1 в любой мере длины), то в этом случае отрезок ОЕ будет определять не только точную численную величину длины заданной окружности к единичному диаметру как уже конкретное число «p» с заданной степенью точности, определяемой принятым количеством шагов алгоритма. Так, если сделать 5 шагов алгоритма (по 3 операции в каждом шаге), то линейный отрезок ОЕ будет выражаться численной величиной 3,14. При выполнении 8 шагов он будет равен числу 3,1241572. А при выполнении 11 шагов величина отрезка ОЕ будет выражаться числом 3,1415923, что в сравнении с трансцендентным числом «p» дает погрешностьd=0,000011%.

Таким образом можно построить линейный отрезок численной величиной «p» с любой наперед заданной степенью точности.

Особенность такой системы построений линейного отрезка численной величиной «p» в том, что эта система позволяет выполнить все построения простейшими инструментами: циркулем и линейкой без делений простыми засечками на координатной оси.

Теоретическая основа данных геометрических построений позволяет получить исключительно предельно точный отрезок численной величиной «p», что подтверждается аналитическими выкладками. Однако, достигаемая точность результата во многом зависит от тщательности проводимых построений и точности применяемого инструмента.