ИННОВАЦИИ БИЗНЕСУ

Результат выполнения научно-исследовательской работы.

Прочность бетона на растяжение является важнейшей характеристикой, определяющей трещиностойкость и несущую способность конструкций. Для ее определения применяются различные способы, дающие часто несопоставимые результаты. Обычно прочность бетона на растяжение находят по данным испытания бетонных призм или цилиндров, растягиваемых за концевые уширения или за стержни, закладываемые в образцы при бетонировании. В этих случаях трудно добиться осевого приложения растягивающей силы, при котором исключался бы эксцентриситет в приложении нагрузки.

Необходимость создания точной центрировки заставляет усложнять конструкцию захватных приспособлений разрывных машин или испытательных установок, что затрудняет оперативный контроль прочности бетона на растяжение по вышеназванной методике в производственных условиях. Использование же самоцентрирующихся захватных приспособлений искажает фактическую прочность бетона на растяжение, так как происходит перераспределение усилий со слабых участков на более прочные. Другой известный способ определения прочности бетона на растяжение заключается в том, что бетонные палочки испытывают на изгиб, после чего полученные данные с помощью коэффициента «К» приводят к случаю осевого растяжения (ГОСТ 10180). Недостатком данного метода является то, что коэффициент «К» принимается постоянным. В действительности он различен для разных марок бетона.

Более целесообразным представляется косвенный способ испытания бетонных образцов на растяжение. Основан он на решении задачи Герца из теории упругости, в которой рассматривается цилиндрический идеально упругий образец. При его нагружении на диаметрально противоположных поверхностях возникают равномерно распределенные растягивающие силы. Они вызывают в вертикальной плоскости загружения плюсовые равномерно распределенные напряжения, которые действуют перпендикулярно к вертикальной плоскости и равны:

, (1)

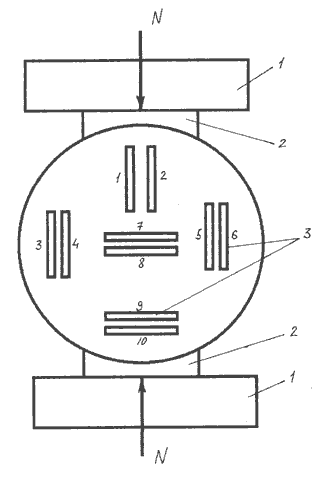
где:

n- сила нагружения;

d, h -соответственно диаметр и высота образца.

Напряженное состояние цилиндрических бетонных образцов диаметром 150 и 300 мм было исследовано при помощи проволочных тензодатчиков сопротивления, наклеенных на основания образцов (рисунок). По их показаниям были получены величины относительных деформаций бетона прочностью 25-30 МПа. Как показали результаты замеров, на первых этапах загружения деформации развивались неравномерно. Перед появлением вертикальной трещины они выравнивались, достигая величин (14-15).10 ^-5 (таблица 1), что равно предельной растяжимости бетона прочностью 20-30 МПа.

Таблица 1

Относительные деформации в образце бетона прочностью 25 МПа

Схема испытания бетонного цилиндрического образца:

1 - плита пресса;2 - фанерные прокладки;3 - тензодатчики

По данным тензодатчиков, наклеенных параллельно вертикальной оси цилиндрического образца, получена эпюра деформаций сжатия. Наибольшая их величина наблюдалась по центру сечения, уменьшаясь к краям образца. Сравнивали также теоретические и опытные величины абсолютных деформаций бетона в местах постановки тензодатчиков.

В задаче Герца даются теоретические величины упругих смещений любой точки относительно осей О ₁x ₁ y ₁, начало которых принято в месте приложения нижней вертикальной силы к поверхности цилиндра:

(2)

(3)

Для сравнения с опытными показаниями тензодатчиков, приведенным к абсолютным деформациям по их длине, определяли теоретические величины разности смещений точек начала и конца датчиков относительно осей О ₁x ₁ y _1,представляющие абсолютныедеформации бетона на тех же участках.Вчастности, были определены теоретические и опытныевеличины разности перемещений начальной и конечной точек вертикальных тензодатчиков № 1 и 2 (принято среднее арифметическое значение показаний этих тензодатчиков) и горизонтального тензодатчика №10 относительно осей О ₁x ₁ y ₁ (таблица2).

Таблица 2

Опытные и теоретические значения абсолютных деформаций бетона

на торце цилиндра (х 10 ^-5 см)

Так как углыj₁иj₂приняты равными нулю, формула (2) упрощается:

, (4)

где:

m- коэффициент Пуассона, принятый равным 0,16;

r ₁ -расстояние от верхней и нижней точек тензодатчиков до верхней точки приложения силыn;

r ₂ -то же, до нижней точки приложения силыn;

r ₃ -расстояние от нижней грани тензодатчика до центра основания цилиндрического образца.

Как видно из таблицы 2, теоретические значения абсолютных деформаций отклоняются от опытных значений на 47,5-66,8%. Такое расхождение можно объяснить тем, что в задаче Герца рассматривается идеально упругий диск. Бетонный цилиндр не отвечает этим условиям. Поэтому в формулу для определения прочности бетона на растяжение необходимо вводить коэффициент К ₁, учитывающий упругопластические свойства бетона. Для его нахождения сравнивали опытные прочности бетона при растяжении призм, уширенных на концах, с прочностями бетона, полученными раздавливанием цилиндров.

Призмы и цилиндры изготавливали из одних и тех же замесов бетона и хранили до испытания в идентичных условиях. Коэффициент К ₁ получен равным 0,55.

При испытании цилиндров из бетонов прочностью 20-30 МПа возникала одна вертикальная трещина. В образцах из более прочного бетона 40-50 МПа также возникала одна трещина, но с незначительным раздроблением бетона у поверхности касания цилиндра с фанерными прокладками, которые изготавливали из трехслойной фанеры толщиной 5 мм, шириной 38 мм и длиной 310 мм. После испытания 30 цилиндрических образцов прокладки не были повреждены.

Представляется целесообразным испытывать цилиндры меньших размеров, так как величина их не оказывает заметного влияния на результаты определения прочности бетона на растяжение, но при этом получаются определенные выгоды (экономия материалов и энергозатрат на испытания, удобство работы с малыми образцами и др.).

Методика определения прочности бетона на растяжение методом раздавливания цилиндрических образцов по образующим проста и может быть рекомендована для строительных лабораторий. При этом в формулу (1) нужно ввести коэффициент К ₁=0,55, учитывающий особенности бетона как упругопластичного материала:

,

где:

n- разрушающее усилие, кг;

d, h- диаметр и высота цилиндра, см.