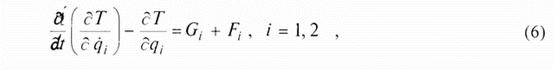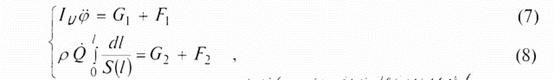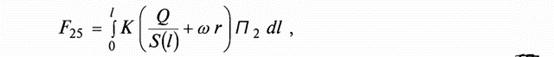ПОДРОБНАЯ ИНФОРМАЦИЯ
Заявку на получение дополнительной информации по этому проекту можно заполнить здесь.
|
Номер 11-008-01 |
|
Наименование проекта Математическая модель динамического лопастного радиального насоса |
|
Назначение Исследование общих закономерностей гидродинамических процессов в динамических лопастных насосах. |
|
Рекомендуемая область применения Решение задачи оптимизации геометрических и технико-экономических параметров динамических лопастных радиальных насосов. |
|
Описание
Результат выполнения научно-исследовательской работы. В целях дальнейшего широкого исследования динамических лопастных насосов на базе уравнений Лагранжа 2-го рода строится математическая модель насоса - система дифференциальных уравнений, позволяющая проводить моделирование гидравлических процессов в насосе в достаточно общей постановке. При построении математической модели насоса рассматривается динамическая система, состоящая из ротора насоса, жидкой среды, движущейся в насосе, ротора приводного двигателя и приводного механизма. Принимаются следующие основные предположения: поток в проточном канале рабочего колеса одномерный и осредненный по поперечному сечению канала; жидкая среда представляет собой несжимаемую вязкую жидкость. Вектор абсолютной скорости
Кинетическая энергия dt элементарного объема при этом определяется как сумма кинетических энергий переносного ( dt u) и относительного ( dt w ) движений:
где dm = rrs( l) dj; r и j - параметры цилиндрической системы координат; s( l) - площадь живого сечения элементарного объема, являющаяся функцией длины проточного канала l. Кинетическая энергия жидкости по всей длине проточного канала
где границы интегрирования соответствуют входному (0) и выходному ( l) сечениям канала.
где q - объемный расход жидкости через поперечное сечение канала q = ws( l) Тогда общая кинетическая энергия Т переносного и относительного движения системы имеет вид;
i u- осевой момент инерции системы.
i h- осевой момент инерции вращающихся масс насоса и привода. Введем обобщенные координаты q1 и q2, совместно однозначно определяющие текущее положение элементарного объема жидкой среды относительно неподвижного наблюдателя: q1 = j( t) - угол поворота колеса насоса от начального положения;
Уравнение Лагранжа 2-го рода, описывающее движение системы, имеет вид:
где g i - обобщенные активные внешние силы; f i - обобщенные реакции наложенных связей. Используя (5) и (6), получим систему дифференциальных уравнений
где (7) - уравнение вращения подвижных элементов системы; (8) - уравнение относительного движения жидкой среды в канале, представляющее собой уравнение Бернулли для относительного движения. В качестве обобщенных сил в уравнении (8) рассматриваются силы, действующие на жидкую среду в колесе насоса. g21 - реактивная сила, обусловленная движением отбрасываемых и присоединяемых в единицу времени масс во входном и выходном сечениях (2, 3):
где s1 и s2 - площади входного и выходного сечений; g22 - проекция на касательную к оси канала равнодействующей силы гидродинамического давления, действующей на ограничивающие элементарный объем сечения:
где p - гидродинамическое давление на поверхностях площадью s( l), ограничивающих элементарный объем; g23 - проекция на касательную к оси канала силы веса жидкости:
где z1 и z2 - ординаты центра масс входного и выходного сечений; f24, f25 - силы трения среды об ограничивающие ее поверхности канала: f24 - на подвижных поверхностях, f25 - на неподвижных поверхностях;
где П 1 - периметр подвижной поверхности; К - коэффициент трения, зависящий от температуры и скорости.
где П 2 - периметр неподвижной поверхности. В уравнении (7) обобщенные g1 и f1 соответствуют интегральным моментам указанных сил относительно оси вращения. Уравнения (7) и (8) полностью описывают переходные процессы движения системы с учетом сделанных предположений. На базе полученных уравнений могут исследоваться различные переходные процессы от включения насоса до наступления стационарных состояний течения жидкости, влияние параметров насоса на гидродинамические параметры движущейся среды, а также решаться задачи оптимизации геометрических параметров насоса при различных режимах работы насоса и реологических свойствах перекачиваемых сред. |
|
Преимущества перед известными аналогами Аналоги не известны. |
|
Стадия освоения Внедрено в производство |
|
Результаты испытаний Технология обеспечивает получение стабильных результатов |
|
Технико-экономический эффект Снижение трудоемкости расчетов в 3 раза, обеспечивается высокое качество и полнота результатов. |
|
Возможность передачи за рубеж Возможна передача за рубеж |
|
Дата поступления материала 04.01.2001 |
Инновации и люди

У павильонов Уральской выставки «ИННОВАЦИИ 2010» (г. Екатеринбург, 2010 г.)

Мероприятия на выставке "Инновации и инвестиции - 2008" (Югра, 2008 г.)

Открытие выставки "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)

Демонстрация разработок на выставке "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)
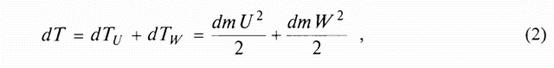
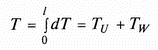



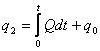 - количество жидкой среды, прошедшей через поперечное сечение канала.
- количество жидкой среды, прошедшей через поперечное сечение канала.