ИННОВАЦИИ БИЗНЕСУ

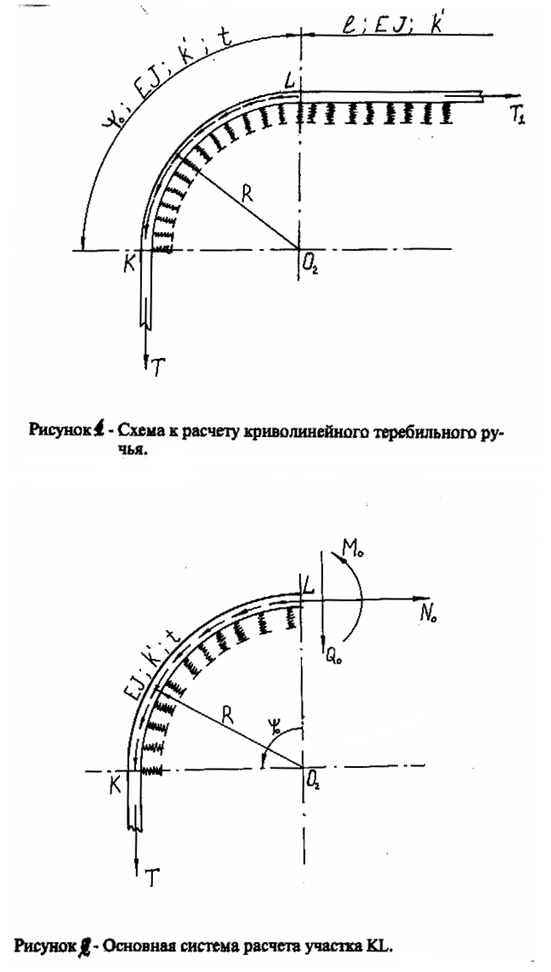
Результат выполнения НИР.

Расчетная схема выбирается при следующих допущениях:

- стебли льна рассматриваются как упругое основание;

- модуль продольной упругости Е и момент инерции поперечного сечения ремняпостоянны по длине ремня;

- коэффициент податливости упругого основания к ¹ является величиной постоянной как на криволинейном, так и на прямолинейном участках ремня;

- продольная ось ремня на криволинейном участке до деформации очерчена по дуге окружности.

Верхний ремень рассматривается как брус, лежащий на упругом основании, которое подчиняется гипотезе Фусса-Винклера: между реакцией основания и просадкой существует пропорциональная зависимость. На основании изложенного расчетная схема принимается следующей (рисунок1).

На схеме обозначены следующие величины:

Т, Т ₁- натяжение ремня ведущей и ведомой ветви;

l -длина прямолинейного участка ремня:

y₀- угол криволинейного участка;
ej -жесткость поперечного сечения ремня при изгибе;

к' - коэффициент податливости упругого основания;

t- интенсивность силы трения, которая принимается равномерно распределенной по дуге криволинейного участка ремня и условно приводится к нейтральной оси этого участка.

Задача определения величины и закона распределения давления со стороны верхнего ремня на стебли льна сводится к определению величины и закона изменения радиального перемещенияw(y)на криволинейном участкеkl.Зная зависимостьw(y)и на основании гипотезы Фусса-Винклера можно записать следующее:

q(y)=-к·w(y) (1),

где q(y)- реакция упругого основания на криволинейном участке;

к - коэффициент упругого основания, который можно определить по формуле:

к= к'·Вр (2),

где к' - коэффициент податливости упругого основания. Значение этого коэффициента зависит от физико-механических свойств льна. По физическому смыслу этот коэффициент равен нагрузке, необходимой для прожатия единицы площади упругого основания на единицу глубины.

Вр - ширина ремня.

Зная величину q(y),можно определить распределенную нагрузку, с которой ремень действует на упругое основание. Очевидно, что она будет равна по абсолютной величине реакции упругого основания и направлена в противоположную сторону:

р(y)-q(y)=кw(y),

где р(y) - распределенная нагрузка со стороны ремня на упругое основание (стебли льна) на криволинейном участке. Разделив эту величину на ширину ремня, получим значение искомого давления.

Задача определения функцииw(y) является статически неопределимой. Основная система представлена на рисунке 2.

Определим значение прогиба ремня на криволинейном участке. Так как на этом участке, определяемым угломyо, ремень изогнут по дуге окружности, то для решения данной задачи необходимо вывести уравнение изгиба кривого бруса на упругом основании, для чего воспользуемся дифференциальным уравнением оси обычного изогнутого бруса:

d ²(w)+w(y)=-М(y)r ²(4),

dw^{2 ej}

гдеw(y) -радиальное перемещение бруса; ej - изгибная жесткость поперечного сечения бруса; r - радиус кривизны бруса; М(y) - изгибающий момент.

Составив уравнение элемента кривого бруса и получив дифференциальные зависимости между внутренними силовыми факторами и нагрузкой в кривом брусе, используем их для преобразования дифференциального уравнения (4) в дифференциальное уравнение кривого бруса на упругом основании, которое будет иметь следующий вид:

d ⁵w+2 d3w+(1+ kr ⁴) dw= -tr ⁴ (5),

dy⁵dy^{3 ej}dy^ej

Находя частное решение уравнения (5), соответствующее его правой части, после преобразований и необходимых подстановок общее решение будет иметь следующий вид:

w(y)=С ₁+С ₂e ^qyсosby+c ₃e ^aysinby+c ₄e ^-qycosby+ c ₅e- ^aysinby-ytr ⁴(6),

(ej-kr ⁴)

где С ₁,С _2, С _3,С _4, С ₅ - постоянные интегрирования, которые определяются из граничных условий при совместном рассмотрении деформированного состояния криволинейного и прямолинейного участков; а,b- действительные и мнимые корни характеристического уравнения, соответствующего уравнению (5) с правой частью, равной нулю.

Значение прогиба ремняw(y), вычисленное по формуле (6) после подстановки в уравнение (3) позволит определить распределеннуюнагрузку со стороны ремня на стебли льна и закон ее распределения на криволинейном участкеklс учетом натяжения ремней, их жесткости, жесткости стеблей льна, которые находятся между теребильными ремнями. Разделив это значение на ширину ремня, получим величину искомого давления.