ИННОВАЦИИ БИЗНЕСУ

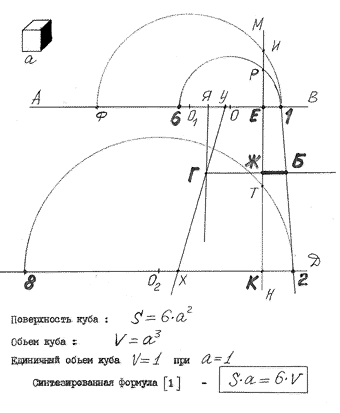
Предложен предельно простой способ решения задачи удвоения объема куба без применения каких-либо вычислительных операций. При этом, как показано на рисунке, производят следующие геометрические построения.

1. Проводят горизонтально две параллельные линии АВ и СД.

2. Проводят вертикальную линию МН, которая перпендикулярна линиям АВ и СД и пересекает их в точках Е и К соответственно.

3. Откладывают на линии АВ вправо от точки Е единичный отрезок Е ₁, равный величине ребра куба единичного объема (ребро а), а влево от точки Е - отрезок Е6, равный шести отрезкам Е ₁.

4. Отрезок 6-1 делят пополам (точка О) и из точки О как из центра циркулем проводят полуокружность радиусом О1, которая пересечет линию МН в точке Р.

5. Откладывают на линии АВ от точки Е влево отрезок УЕ, равный отрезку ЕР.

6. Откладывают на линии СД вправо от точки К отрезок К ₂, равный по величине двум отрезкам Е1, а влево от точки К - отрезок К8, равный по величине двадцати четырем отрезкам Е1.

7. Отрезок 8-2 делят пополам (точка О ₂), и из точки О ₂ как из центра циркулем проводят радиусом 8О ₂ полуокружность, которая пересечет линию МН в точке Т.

8. Откладывают на линии СД влево от точки К отрезок ХК, равный отрезку ТК.

9. Проводят прямые линии через точки У и Х, а также через точки 1 и 2.

10. Откладывают на линии АВ влево от точки 6 отрезок Ф6, равный по величине отрезку Е6, и из середины отрезка Ф1 в точке О ₁ циркулем проводят полуокружность радиусом ФО ₁, которая пересечет линию МН в точке И.

11. Откладывают на линии АВ влево от точки Е отрезок ЕЯ, равный по величине отрезку ЕИ.

12. Проводят через точку Я луч, параллельный линии МН, который пересечет линию УХ в точке Г.

13. Проводят луч из точки Г, параллельный линиям АВ и СД, который пересечет линию 1-2 в точке Б, а линию МН - в точке Ж. Полученный отрезок БЖ по величине абсолютно точно будет равен величине ребра куба, удвоенного по объему относительно заданного единичного объема куба.

При величине отрезка Е1, равного единице, величина отрезка БЖ составит 1,2599210498949… (трансцендентное число, равное ).

Теоретическое обоснование данных геометрических построений базируется (см.рисунок) на синтезированной формуле[1], показывающей простую зависимость величины поверхности куба от величины его же объема.