ИННОВАЦИИ БИЗНЕСУ

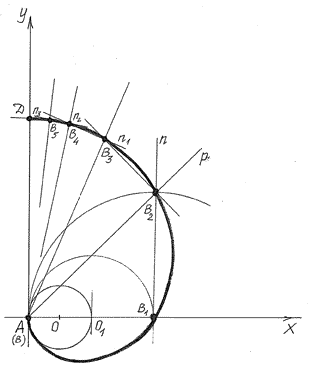
Предложено строить специальную кривую - пиоиду, отображающую точную развертку заданной окружности в отличие от прежней лекальной кривой - эвольвенты.

Пиоидой окружности называется траектория подвижного конца заданной окружности при перемещении центра окружности вдоль луча, на котором расположен один неподвижный конец этой окружности и ее первоначальный центр.

Графическое построение пиоиды весьма простое (см.рисунок).Так, если на осях координат У и Х с центром в точке А задана окружность с центром в точке О, то для построения пиоиды и одновременно с этим построения полной развертки заданной окружности выполняют следующие шаги.

1. Принимают в точке А (центр координатной оси) неподвижную точку заданной окружности с центром в точке О. Вместе с этим подвижная точка В этой же окружности вначале находится также на месте расположения точки А.

2. После перемещения точки О - центра заданной окружности - вдоль луча из точки А через точку О (например, в точку О ₁) из точки О ₁ как из центра проводят полуокружность радиусом АО ₁. И тогда точка В ₁ как точка пересечения полуокружности с лучом из точки А явится второй точкой, принадлежащей кривой - пиоиде. При этом заданная окружность с центром в точке О развернется в дугу АВ ₁.

3. При последующем перемещении центра заданной окружности вдоль луча из точки А (например, в точку В ₁) вновь проводят полуокружность - дугу с центром в точке В ₁ радиусом АВ ₁, которая пересечет в точке В ₂ перпендикулярn, восстановленный из точки В ₁ к линии АВ ₁. И тогда точка В ₂ явится очередной точкой, принадлежащей кривой - пиоиде. При этом заданная окружность развернется в дугу АВ ₂.

Точку В ₂ кривой - пиоиды, как и последующие ее точки, можно получить и несколько иным способом по системе ПОКО.

Так, для получения точки В ₂ выполняют следующие шаги:

а) из точки А проводят луч-биссектрису р, делящую угол УАХ пополам;

б) из точки В ₁ восстанавливают перпендикулярnк линии АВ ₁, который пересечет в точке В ₂ луч-биссектрису из точки А.

4. Для получения последующих точек кривой - пиоиды (например, точки В ₃) снова делят угол УАВ ₂ пополам лучом-биссектрисой из точки А, а из точки В ₂ восстанавливают перпендикуляр к линии АВ ₂, который в пересечении с лучом-биссектрисой и даст точку В ₃.

Конечная точка пиоиды как траектории подвижного конца заданной окружности лежит на вертикальной оси координат УА. Это точка Д. Она получается при последовательном конечном приближении точки пересечения луча-биссектрисы с соответствующим перпендикуляром к предыдущему лучу-биссектрисе.

При этом заданная окружность с центром в точке О полностью развертывается в прямую линию АД.

Точность данных геометрических построений практически безгранична и зависит только от точности применяемых инструментов, количества лучей-биссектрис, делящих углы пополам, и тщательности выполняемых работ.