ИННОВАЦИИ БИЗНЕСУ

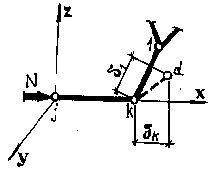
Влияние нагрузки передается в ненагруженную часть фермы непосредственно, а также через смещение узлов. Передача нагрузки может быть учтена введением коэффиицента линейной жесткости. Рассмотрим стержень jk - любой стержень пространственной фермы. Проведем координатные оси через узел j так, чтобы ось х совпала с осью стержня (см. рисунок). Стержень kl - один из стержней, с которыми стержень jk соединен в узле k. Таких стержней может быть n. Отрезок kd - перемещение в пространстве узла k в процессе работы фермы. Обозначим: a, b, c - направляющие косинусы стержня kl относительно осей х, y, z соответственно; p, r, s - направляющие косинусы перемещения kd. Проекция отрезка kd на ось k1 или перемещение точки k относительно kl вдоль его оси будет определяться умножением величины отрека kd на косинус пространственного угла. Это же перемещение одновременно будет равно частному от деления величины усилия в стержне kl (n1) на его линейную жесткость (m1). Линейной жесткостью названа величина, характеризующая сопротивление стержня линейному смещению узла. Численно линейная жесткость равна силе, вызывающей перемещение, равное 1. Согласно общих основ метода узловых жесткостей: m=жi, где ж - коэффициент линейной жесткости, i - линейная погонная жесткость. Если узел 1 неподвижен, то ж=1. Если узел 1 перемещается свободно, то ж=0. Таким образом, 0<ж>1. Так как kd=бк/р, то можно записать уравнение, в которое войдут: n1. бк, m, а также направляющие косинусы векторов k1, kd. Если взять проекции всех усилий в стержнях, соединенных в узле k со стержнем jk на координатные оси, то образуется система из трех уравнений. Искомое усилие в стержне kl может быть найдено из совместного решения системы из четырех уравнений, перечисленных выше. Величину линейной жесткости стержня jk можно получить из рассмотрения его работы в системе. Если положить перемещение узла j вдоль jk равным 1, то бк=l-m/i, где m - линейная жесткость стержня jk, т.е. сила, вызывающая б=1. Отсюда определяется m, а также коэффициент линейной жесткости, который представляет рекуррентную величину, часть непрерывной цепочки зависимостей, Все звенья этой цепочки могут быть определены, если задаться вначале значениями всех ж=1 ( за исключением концевых стержней системы с известными значениями ж) и затем пройтись по цепочке несколько раз, постепенно уточняя коэффициенты. Это может быть получено ЭВМ.